Table Of Content
The ability to recognize if results can be generalized to different circumstances or group features thus serves as another advantage for this type of design. In an RCT there are a very limited number of experimental conditions (“arms” in RCT terminology)—usually just two or three—and the objective is to compare the individual experimental conditions to each other directly. By contrast, in a factorial experiment the objective is generally not to compare individual conditions to each other. (I’ve found that this is very counterintuitive for many intervention scientists!) Instead, for most effects, combinations of experimental conditions are compared. In an RCT an “active” treatment arm or condition is statistically contrasted with a “control” treatment arm or condition (Friedman, Furberg, & Demets, 2010). The two conditions should be identical except that the control condition lacks one or more ICs or features that are provided to the active condition.

Assigning Participants to Conditions
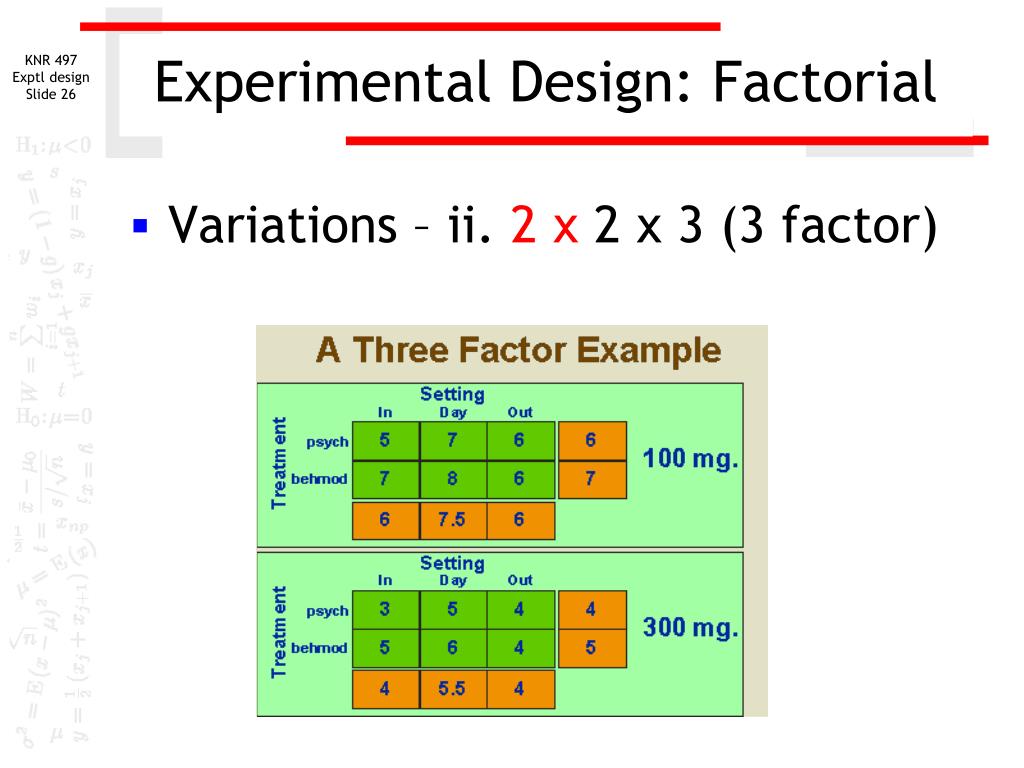
This would be obtained by comparing the mean of the conditions in which the increasing physical activity component is included (1,2,5, and 6) to the mean of the conditions in which this component is not included (3,4,7, and 8). In Table 3, this is the mean of unshaded conditions compared to the mean of the shaded conditions. After all the trials were performed, the wt% methanol remaining in the biodiesel and number of theoretical stages achieved were calculated. The figure below contains the DOE table of trials including the two responses. The names of each response can be changed by clicking on the column name and entering the desired name.
How to Interpret Causal Effects
This experimental design method involves manipulating multiple independent variables simultaneously to investigate their combined effects on the dependent variable. A more realistic experiment might involve the same blocking structure but three factors—each with a specified range—and a goal to determine how the response is impacted by the factors and their interactions. We want to study the factors in combination; otherwise, any interactions between them will go undetected and the statistical efficiency to estimate factor effects is reduced. A lot of people seem to think that factorial experiments require huge amounts of experimental subjects. Maybe they think of a factorial experiment in RCT terms, and therefore think that ultimately the experimenter will be comparing individual experimental conditions.
Whether to Use an RCT or a Factorial Design
Optimization of harvest and extraction factors by full factorial design for the improved yield of C-glucosyl xanthone ... - Nature.com
Optimization of harvest and extraction factors by full factorial design for the improved yield of C-glucosyl xanthone ....
Posted: Wed, 11 Aug 2021 07:00:00 GMT [source]
From the example above, suppose you find that as dosage increases, the percentage of people who suffer from seizures increases as well. You also notice that age does not play a role; both 20 and 40 year olds suffer the same percentage of seizures for a given amount of CureAll. From this information, you can conclude that the chance of a patient suffering a seizure is minimized at lower dosages of the drug (5 mg). The second graph illustrates that with increased drug dosage there is an increased percentage of seizures, while the first graph illustrates that with increased age there is no change in the percentage of seizures. Both of these graphs only contain one main effect, since only dose has an effect the percentage of seizures. Whereas, graphs three and four have two main effects, since dose and age both have an effect on the percentage of seizures.
This design involves dividing participants into blocks based on a specific characteristic, such as age or gender, and then randomly assigning participants within each block to one of two or more treatment groups. For example, to estimate the main effect of keeping a food diary, you would compare the mean of all of the conditions in which keeping a food diary is set to No (Conditions 1—4) to the mean of all of the conditions in which keeping a food diary is set to Yes (Conditions 5—8). In Table 2, this is the mean of the unshaded conditions compared to the mean of the shaded conditions.
An analysis of environment effect on ethanol blends with plastic fuel and blend optimization using a full factorial design ... - Nature.com
An analysis of environment effect on ethanol blends with plastic fuel and blend optimization using a full factorial design ....
Posted: Thu, 15 Dec 2022 08:00:00 GMT [source]
Analysis
However, because laboratory conditions are not always representative of real-world conditions, the results of these experiments may not be generalizable to the population at large. This design involves randomly assigning participants to one of two or more treatment groups, with each group receiving one treatment during the first phase of the study and then switching to a different treatment during the second phase. There is no guarantee that (i) the experiment can achieve good power, (ii) the model form is valid and (iii) the criterion reflects the objectives of the experiment. However, in an experiment with constraints, these assumptions can usually be specified reasonably. For both criteria, numerical heuristics are used in the optimization but they do not guarantee a global optimum.
Experimental research design should be used when a researcher wants to establish a cause-and-effect relationship between variables. It is particularly useful when studying the impact of an intervention or treatment on a particular outcome. In many settings, the goal is to learn about whether and how factors affect the response (i.e., whether β1 and/or β2 are non-zero and, if so, how far from zero they are), in which case the D-criterion is a good choice. In other cases, the goal is to find the level of the factors that optimizes the response, in which case a design that produces more precise predictions is better. The I-criterion, which minimizes the average prediction variance across the design region, is a natural choice.
Factors, Main Effects, and Interactions
Participants are given one of three different drug doses, and then asked to either complete a simple or complex memory task. To have a total of 3 trials of each, the user should add 2 replicates in this menu. Typically, if the same experimentation will occur for 3 lab periods, 2 replicates will be added. Replicates are repeats of each trial that help determine the reproducibility of the design, thus increasing the number of trials and accuracy of the DOE. To add replicates, click the "Replicate design" radio button in the "Modify Design" menu.
If an investigator anticipates severe problems from including a particular factor in an experiment, perhaps due to its nature or the burden entailed, s/he should certainly consider dropping it as an experimental factor. Indeed, the MOST approach to the use of factorial designs holds that such designs be used to decompose a set of compatible ICs, ones that might all fit well in an integrated treatment package (to identify those that are most promising). That is, one should include only those ICs that are thought to be compatible, not competitive. The vast majority of investigations of treatment efficacy and effectiveness over the past 30–40 years have used the randomized controlled trial (RCT) design. While factorial designs offer some advantages for certain research goals, their use can entail critical decisions regarding design, implementation, analysis, and interpretation.
If an investigator decides to use a factorial design, s/he has numerous choices to make, including choices about the number and types of factors to include. These equations can be used as a predictive model to determine wt% methanol in biodiesel and number of theoretical stages achieved at different operating conditions without actually performing the experiments. However, the limits of the model should be tested before the model is used to predict responses at many different operating conditions. In addition to the above effects plots, Minitab calculates the coefficients and constants for response equations. The response equations can be used as models for predicting responses at different operating conditions (factors).
As opposed to an RCT, where the focus is on demonstrating effects that are highly unlikely to be due to chance, the screening experiment is focused on relative promise of the tested ICs. In many factorial designs, one of the independent variables is a non-manipulated independent variable. An example is a study by Halle Brown and colleagues in which participants were exposed to several words that they were later asked to recall (Brown, Kosslyn, Delamater, Fama, & Barsky, 1999)[1]. Some were negative health-related words (e.g., tumor, coronary), and others were not health related (e.g., election, geometry).
For example, suppose that you have a reactor and want to study the effect of temperature, concentration and pressure on multiple outputs. In order to minimize the number of experiments that you would have to perform, you can utilize factorial design. This will allow you to determine the effects of temperature and pressure while saving money on performing unnecessary experiments. The following Yates algorithm table was constructed using the data from the interaction effects section.
Including additional factors in an experiment might certainly affect the significance tests of a given factor. For instance, if the added factors have very weak effects (i.e., the outcome is unchanged whether the levels are “on” or “off”), then their presence will reduce power because they reduce the degrees of freedom in the estimate of sigma (part of the denominator of the t statistic). The reduction in power will be greater if we control experiment-wise error, due to the larger number of main and interaction effects. Including numerous factors might also increase the occurrence of interactions, which might affect the magnitude of a main effect (despite the lack of correlation between main and interaction effects with effect coding).

No comments:
Post a Comment